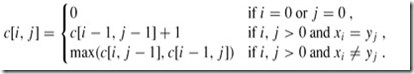一、概念
动态规划策略,一种分治策略。和贪婪策略一样,通常是用来解决最优解问题。分治故名就是将问题分解为几个子问题来解决,动态规划的特点就是分解的子问题中(子问题又可以分解成子问题)每次选择选择最优解。
动态规划主要的特点是在做决定前她知道所有子问题的信息。
动态规划的两个重要要素是:1)最优子结构。2)重叠子问题。
1)最优子结构,这是采取动态规划策略解最优化问题后要做的第一步。所谓最优化子结构是说若问题的一个最优解中包含了子问题的最优解,则该问题具有最优子结构。这个是我们采取动态规划的一个充分条件(当然这个条件也满足贪婪策略),问题出现这个条件就可以考虑采取动态规划。
一般要考虑的因素是:
1.1)最优解里需要解决的子问题数量有多少?
1.2)在判断使用那些子问题时需要进行多少选择?
2)重叠子问题,是指在递归解决方案中,若产生了大量的相同子问题,那么相同的子问题就会被重复计算很多次,这样算法的效率损耗就很大。这个要素是动态规划的优势所在,可以说动态规划就是为解决这种问题而生的(实际上,有记忆的递归算法也可以做到类似的算法改进).
二、解题策略
一般解题的思路为:
1)证明问题的解决方案中包括一个选择,选择之后将留下一个或多个子问题
2)设计子问题的递归描述方式(一般会出现递归公式又称转移方程,这个是解题和算法的关键)
3)证明对原问题的最优解里包括对所有子问题的最优解
4)证明子问题之间有重叠
可以看出1、3、4是为了使得子问题的构建能符合动态规划策略,他们的目的都是为了他构建一个合理恰当的子问题而服务的。但是不同问题构建子问题的思路不尽相同。除了要考虑1.1、1.2的问题外,通常有个比较有效的经验,就是尽量使得这个子问题简单,然后在需要的时候去扩充她.
三、例子
用比较经典的最长公共子序列问题(LCS)。
问题定义如下:两个子序列S1[1..m]和S2[1..n],需要找出他们的一个最长公共子序列(其中子序列不一定必须是连续的)。
解法一:暴力穷举法
思路:
1)检查S1[1..m]中的每一个子序列.
2)看看其是否也在S2[1..n]里的子序列.
3)在每一步记录当前找到的子序列里面最长的子序列.
显然效率非常低下:每个子序列的检查要时间O(n),而共有2^m子序列需要检查,so时间复杂度问O(n*2^m).
那么如何改进呢,由于LCS中存在最优子结构,即所求的最长公共子序列包含子最长公共子序列,所以我们可以尝试使用动态规划来解决问题.
解法二:动态规划
按照解题策略,我们要先构造一个合适的子问题,根据第二点提到的,我们构建一个尽量简单的子问题,然后在去扩展.在LCS中,便有:
1)先寻找最长公共子序列的长度.
2)扩展寻找长度的算法来获得最长公共子序列.
由上可以得到一个递归表达式:
( c[i,j]表示长度为i的S1和长度为j的S2的最长公共子序列. xi表示表示S串中的第i个字符. )
上面递归式的推倒通过画图可以很容易得出.
代码:

char b[50][50]; //记录路径图,方便输出LCS
int c[50][50]; //c[i][j]存长度为i的x串和长度为j的y串的LCS的长度
char x[50], y[50]; //x,y存两个要比对的字符串
void LCS()
{
int m = strlen(x+1);
int n = strlen(y+1);
//初始化
for(int i=1; i<=m; ++i)
c[i][0] = 0;
for(int j=1; j<=n; ++j)
c[0][j] = 0;
for(int i=1; i<=m; ++i)
for(int j=1; j<=n; ++j)
{
if(x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = '\\';
}
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = '|';
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = '-';
}
}
}
//输出LCS
void printLCS(int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == '\\')
{
printLCS(i-1, j-1);
print(x[i] +"");
}
else if(b[i][j] == '|')
printLCS(i-1, j);
else
printLCS(i, j-1);
}
四、小结
LCS的变种还有很多:最长递增/递减子序列、编辑距离等.
动态规划的关键还是以上提到的两个重要的元素:最优子结构和重复子问题.最优化问题中若出现了相关的信息或可以转换到此类问题的则可尝试使用动态规划.但是子问题的构建需要花费一定的思考即构建递归方程式.
但是,动态规划的虽然能做出最"明智的"决定,但她需要对一切"了如指掌"后才能做到,这显然趋于"保守",所以并非所以问题都适用.这个时候其它最优化算法可以被考虑.